Assuming a protein receptor P with a single binding site for the ligand L, such that they interact to transiently form the complex PL, the binding equilibrium can be described by a model of two states with a temperature dependent dissociation constant KD:

where the unimolecular dissociation rate constant koff is inversely related to the lifetime of the protein-ligand complex or, equivalently, the residence time of the ligand in the bound state tres (Fig. 5), whereas the bimolecular rate constant kon is the probability of a productive interaction between the protein and the ligand. At any given time, the fraction of bound protein fPB is given by:
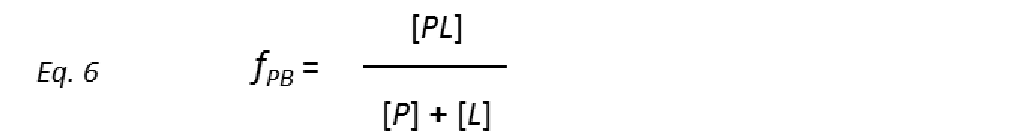
Combining equations 5 and 6 yields
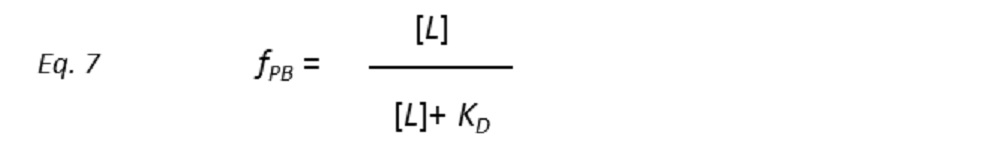
This is one of the fundamental equations that drives the outcome of the NMR experiment. It shows that increasing the ligand concentration [L], the fractional occupation of the receptor-binding site fPB will rise in a hyperbolic function of [L]. In the limit [L] << KD, the fractional population of bound protein is directly proportional to the concentration of the free ligand. In the other extreme, [L] >> KD, the protein receptor is completely saturated by the ligand (fPB = 1). An interesting situation occurs when [L] = KD, that is, the receptor is half-saturated, which means that half of the receptor molecules exist in a one-to-one complex with the ligand. Ligands with weaker affinity have larger KD and so, to saturate the receptor-binding site, the addition of more ligand molecules is required than in the case of a ligand with higher affinity. Thus, by adjusting the receptor and ligand concentrations, it is possible to “select” the maximum KD for an optimum observable NMR signal. This tuning of detection threshold is very useful in ligand-based screening experiments (STD NMR in particular) of large libraries of compounds.
In the free state, both receptor and ligand retain their intrinsic NMR parameters (e.g. chemical shifts, relaxation rates, translational diffusion coefficients). In each other’s presence, the mutual binding affinity of ligand and receptor drives an exchange process that toggles both sets of molecules between the free and complexed states. At equilibrium, the transient presence of the ligand molecule at the protein site is responsible for chemical exchange, characterized by the exchange kinetic constant kex.

All the ligand-based NMR screening experiments assume that the receptor-ligand binding is in the fast exchange limit. Indeed, this is a necessary condition for ligand-based NMR techniques to be useful, as in the fast exchange limit the equations are enormously simplified, and the total effect of the protein-ligand complex on the NMR parameter is just the weighted sum of its separate contributions (weighted average). Thus, if Q is the NMR parameter, then
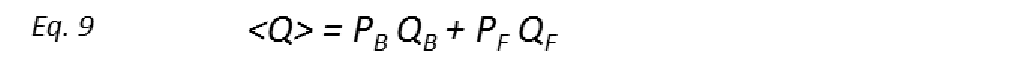
where 〈Q〉 is the observed exchange-averaged parameter between its free (F) and bound (B) states, with respective populations PF and PB. Observed differences between 〈Q〉 and QF provide measurable evidence of receptor binding and often an indicator of a “hit” in screening of a large library of compounds. The ability to detect binding with adequate sensitivity depends critically on the bound state contributions (PBQB) being significantly larger than those from the free state (PFQF). Since typical screening conditions where [L]T >> [P]T are used automatically make PB << PF, it is therefore necessary that 〈Q〉 is amplified in the bound state (i.e. QB >> QF). On the other hand, if kon is well approximated by a diffusion-limited value (107-109 M-1s-1), then the slowest kex constants lie within the 103 < kex < 105 s-1 range for weak-affinity ligands (KD in the μM range). Since ligand-based NMR screening methods are primarily 1H based, kex would consequently exceed most differences in intrinsic 1H relaxation rates and rotating frame precession frequencies, thus supporting the validity of the fast exchange assumption.